信号処理入門（１）：同期加算の実装

佐藤幸男・佐波孝彦『信号処理入門』を読み進める。amazonの評価がめちゃくちゃ低くて、まあ確かに数学書や専門書として読むには厳密性に欠けるところがあるのは否めない。しかし今回の俺みたいに信号処理の中身を見ていくにはとてもいいと（少なくとも俺は）思う。というのも、マーケティング分野で統計モデリングやって趣味では楽曲もリリースしてるということで各方面にほんのちょっっっとだけ前提知識があるし、各種証明は割愛されているものの統計学方面から理解できてる部分は多少なりともあるし…ということで。たぶんこれ読んだ後にもうちょっと厳密な書き方してる本もう一冊やれば普通にかなりいい感じになると思う。まあすぐに「信号処理なんもわからん」って言い出すのでご安心ください。

とりあえず第2章で興味深かった同期加算（Synchronous averaging, MATLABではTime-Synchronous Signal Averagingと表記されていた）によるノイズ除去をColaboratory使ってPythonで実装してみる。これは生演奏とか歌唱みたいな同じ信号が得られないようなものではできないだろうし、マーケティング分野でも同じ理由でまずできない。何より測定誤差が大きすぎる。

同期加算は、簡単にいうとノイズ圧縮の手法。前提として、ノイズ部分がガウス性雑音になっていることが条件になる。Wikiの言葉を借りるなら「正規分布（ガウス分布ともいう）と等しい確率密度関数を持つ統計的雑音。言い換えると、ノイズがとる値がガウス分布」であることで、より統計学的な表現をすれば「誤差項が正規分布に従う」ことと同義だと思う。

方法としては、周期的に同じ信号が得られることを前提として（とはいえもちろんそこに乗ってくるノイズは正規分布に従って生成されているだけで毎回異なるもの）、位相を合わせて同じ信号を繰り返し受信し、得られた値を平均することでノイズ部分がキャンセルアウトされて本来の信号部分だけが残る。面白い。やってみたい。やる。

まずは普通に正弦波（sin波）をプロット。

import numpy as np
from matplotlib import pyplot as plt

# 周期2piの正弦波を生成（ 振幅A, 位相θ = 1 ）
t = np.arange(0, 2*2*np.pi, 0.05)
y = np.sin(t)
plt.plot(t,y)

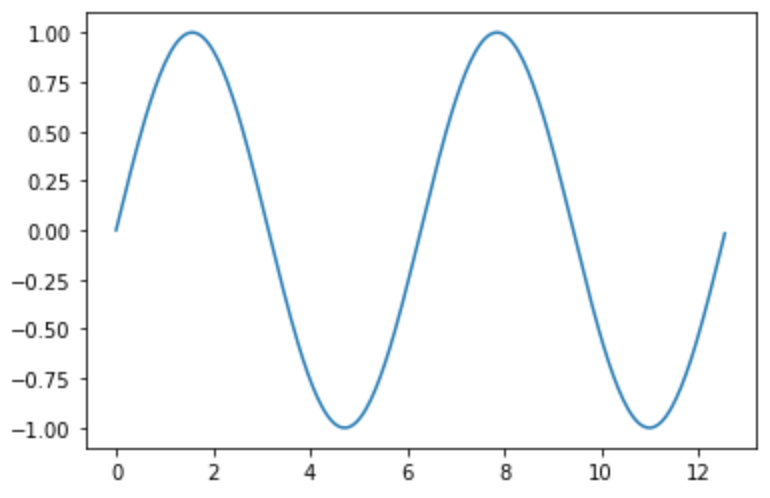
今回は1周期（2π≒6.28）を126回サンプリングした。

ちなみにサンプリング問題について、サンプリングレートを変更することで軽く確認しておく。

import numpy as np
from matplotlib import pyplot as plt

# サンプリングレートを変えてみる
for s,l in zip([1, np.pi/2, np.pi-0.1, np.pi, 2*np.pi], ['1', 'pi/2', 'pi-0.1', 'pi', '2pi']):
  t = np.arange(0, 2*2*np.pi, s)
  y = np.sin(t)
  plt.plot(t,y, label=l)
  plt.legend(loc="lower left")

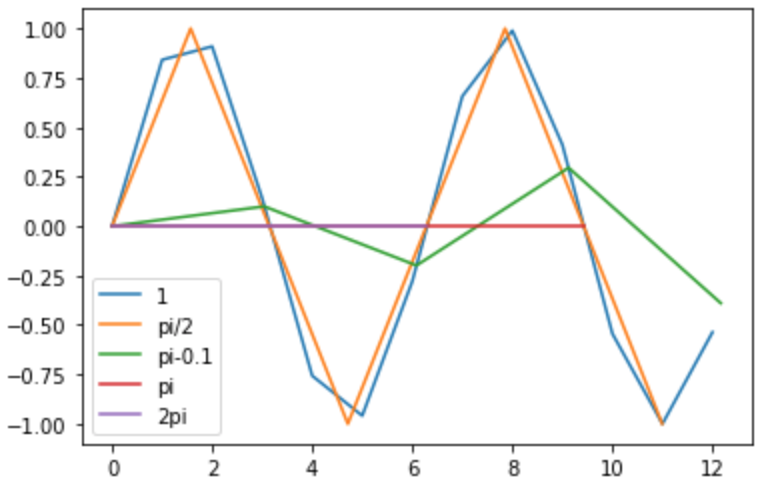
確かに周期Tに対してサンプリング頻度をT/2やTにした場合（今回だとpiと2*pi）は周期に合わせて常に同じ値（今回は0）のみをサンプリングしてしまい直線になっている。T/2より少しでも小さな値（今回はpi-0.1）にすると波が現れる。

今度はここにノイズを載せてみる。試しに（明らかにデカいが）標準正規分布に従ったノイズe~N(0, 1)を載せる。

import numpy as np
from matplotlib import pyplot as plt

# 標準正規分布に従ったノイズ e ~ N(0, 1) を載せてみる
t = np.arange(0,2*np.pi,0.1)
e = np.random.normal(loc=0,scale=1,size=len(t))
y = np.sin(t) + e
plt.plot(t,y)

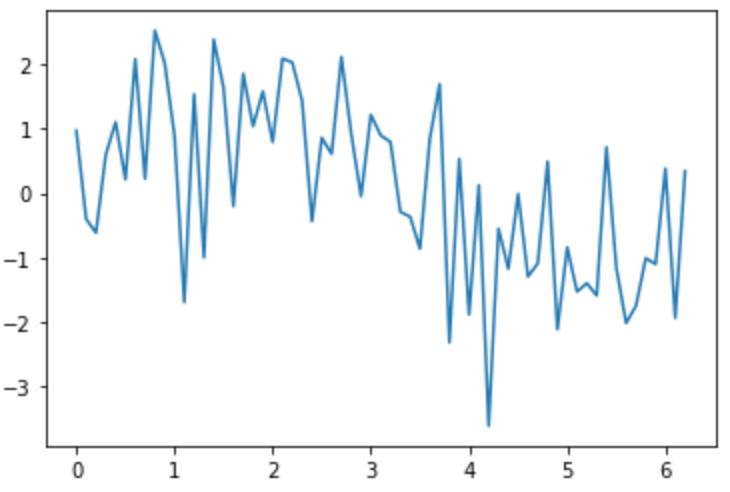
でかすぎる。これでは目視でも本来のトレンドたる正弦波が見えない。本では同期加算によるノイズの圧縮に関して「周波数が高く、その大きさも微量であるならば」という制約条件が付してある。

正規分布はランダムウォークのためその周波数はサンプリングの回数に応じて増加する。取り急ぎサンプリング間隔を短くし、そしてノイズの大きさたる振幅（＝正規分布の分散）を小さくする。

# ノイズ周波数:高(0.0001) ノイズ振幅:大(1)
def generate_noised_sin(seed):
  np.random.seed(seed=seed)
  e = np.random.normal(loc=0,scale=1,size=len(t))
  y = np.sin(t) + e
  return y

def trial(n=1):
  sin = np.zeros(len(t))
  for i in range(n):
    y = generate_noised_sin(seed = i)
    sin = sin + y
  sin = sin / n
  plt.plot(t, sin, label=str(n))
  plt.legend()

t = np.arange(0,2*np.pi,0.0001)
trial(n=1)
trial(n=10)
trial(n=1000)

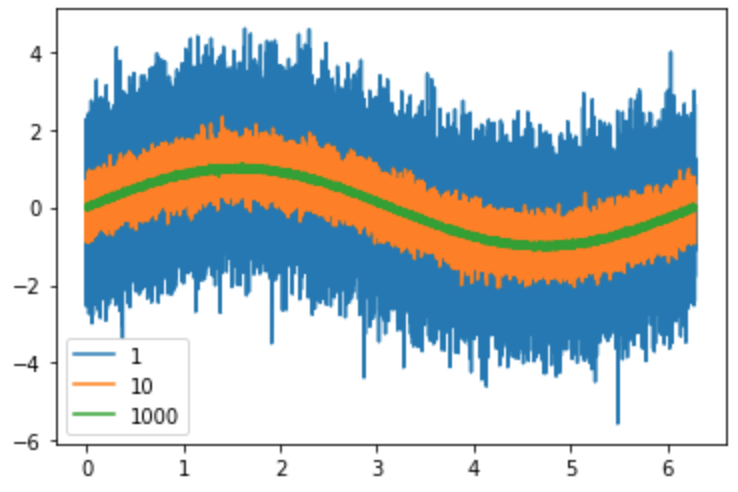
通常のノイズ付き正弦波（青）と、同期加算の試行回数で色分けした結果。10回の同期加算を行った結果（オレンジ）だとそこまでだけど、iterationを増やせばちゃんと削れる。本の通り1000回も回せばかなりノイズ部分は小さくなる。

ノイズ単体の状況も見てみる。単体の信号と、あとはヒストグラムでちゃちゃっとみる。

import numpy as np
from matplotlib import pyplot as plt

# ノイズだけ発生させてヒストグラムを見る。
t = np.arange(0,2*np.pi,0.01)
e = np.random.normal(loc=0,scale=0.01,size=len(t))
plt.plot(t, e)
plt.hist(e)

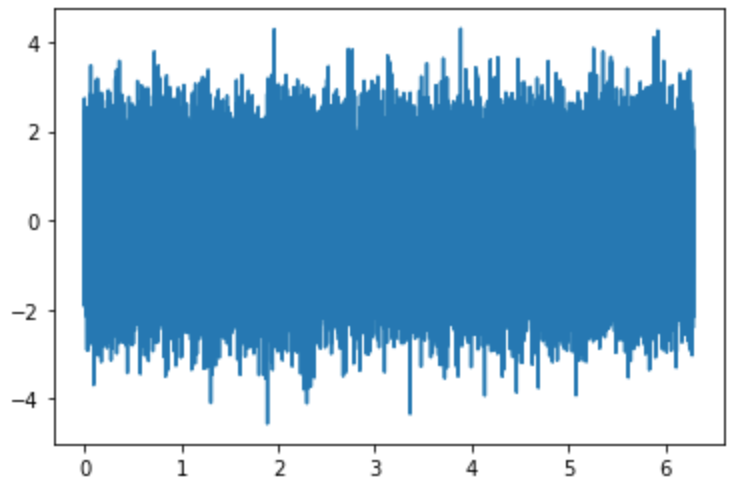
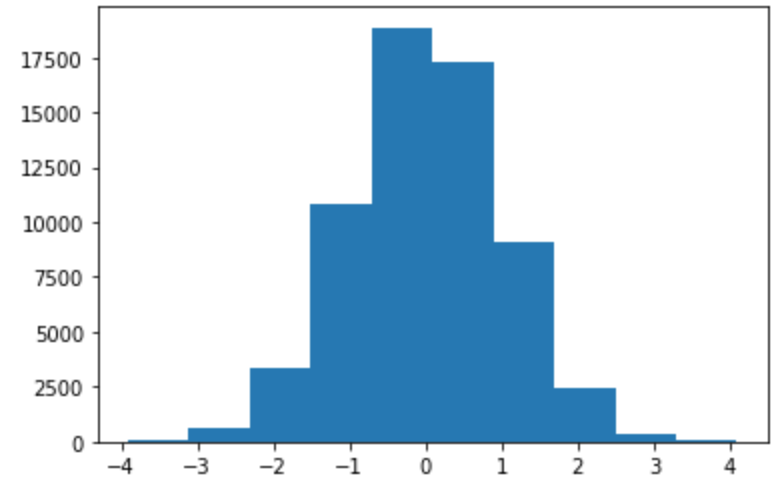
うん、大丈夫ですね。サンプリングの回数の割にはヒストグラムの峰が左にずれてる（＝右に歪んでる）のが気になるけど。

まあとりあえずできたし、なんか明け方になってきちゃったので今日は一旦ここまで。