MATLABでRNN（２）LSTMでSequence-to-One回帰

たまに海外のわけのわからない仕事を受けるんだけど先日”Hi, professor!”から始まる依頼メッセージが来て、フランクすぎて笑ってしまった。プロフェッサー呼びしながらそんなカジュアルな態度で来るのか（だからといって先生とか呼ばれるのは好きじゃないし単純に面白いから別にいいんだけど）。世界的な問題が全く解決しそうにないこの年の瀬でも、こういうふとした一瞬には笑ってしまうものだ。

LSTMでSequence-to-One回帰をやる（MATLABでRNNシリーズ）

前回NARXNETでSequence-to-Sequenceの回帰をやったけどここからが本番で、今回はLSTMでSequence-to-One回帰をやる。つまり時系列データを非集計のまま食わせた上で一つの値を回帰で吐き出す。本当はこの2つの間にLayer Recurrent Neural Network (層再帰型ニューラル ネットワーク, layrecnet）でSequence-to-Sequenceを挟むつもりだったんだけどやってみたらあんまり面白くなかったのでまた今度。

前回扱ったSequence-to-Sequence型の回帰だと事実上タイムステップ T の数だけ目的変数側にもサンプルが生成されるからサンプルサイズ1でも普通にシミュレーションできるんだけど、Sequence-To-One型の回帰というのは T がいくつだろうと N と目的変数のサンプルが一致するのでちゃんとデータを作らないといけない。つまりデータの構造としてサンプルサイズ N × 説明変数の数 J × タイムステップ T の3次元データになるから扱いが面倒くさい。pandasみたいにマルチインデックスにすると生データとしての視認性は高くなるけど代わりに分析はしづらくなる。

MATLABではこういうのはCell型で扱うことになる。number of elements（要はサンプルサイズ）分だけのセル（つまり N × 1 サイズのCell）を作って、各セルの中に J × T サイズのDouble型を突っ込んで、Cell全体で説明変数Xを構成する。

サンプルデータは1〜T 期までの x に回帰係数coefをかけて足し合わせるだけ。今回は説明変数1つ、サンプルサイズ100、Timestep 10で、

nvar = 1; n_y = 1; N = 100; T = 10; 

X = cell(N, nvar); 
Y = cell(N, 1);
bias = 2;
coef = rand(1,nvar);

for n = 1:N
    X{n, 1} = round(rand(nvar, T)*10);
    Y{n, 1} = bias + sum(X{n,1});
end
Y = cell2mat(Y);

この形。biasも乱数で吐いていいんだけど今回はなんとなく2に。変数Y はCell型にしろって書いてあるんだけど、Cellで突っ込むとなぜかエラー吐いて動かないので最後にMatrixに変換してある。

そしてネットワークの構成。今回はシンプルなデータなのでLSTMの隠れ層のユニット数は1で、

% ---02 Setup Network
n_hidunit = 1;

layers = [
    sequenceInputLayer(nvar, 'name', 'Input')
    lstmLayer(n_hidunit,'OutputMode','last', 'name', 'LSTM')
    fullyConnectedLayer(n_y, 'name', 'Feed-Forward')
    regressionLayer('name', 'Output')
    ];

これは結局のところただの回帰なので、個人的にはLSTMの後のfullyConnectedLayerはいらなくて本当は直接Output層のregressionLayerに繋げたいんだけどね。そこのbias, weight = 0, 1とかで固定できればそれでもいいんだけど。

% ---04 Begin Training 
net = trainNetwork(X, Y,layers, options)
yhat = predict(net, X);

e = gsubtract(Y,yhat);
se = e.^2;
mse = sum(se)/N;
rmse = sqrt(mse)

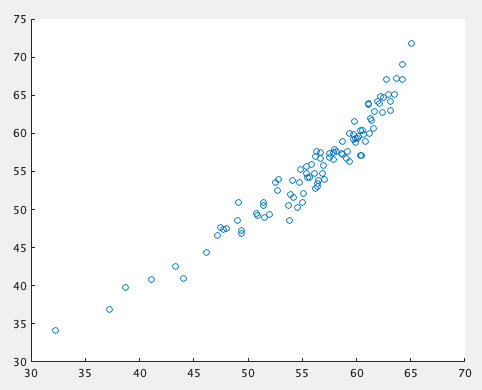
scatter(yhat,Y)

Epoch 12000時点でRMSE = 0.6412、時間はかかるけど結果としては全くもって悪くないですね。

横軸が予測値yhat、縦軸が実測値Y

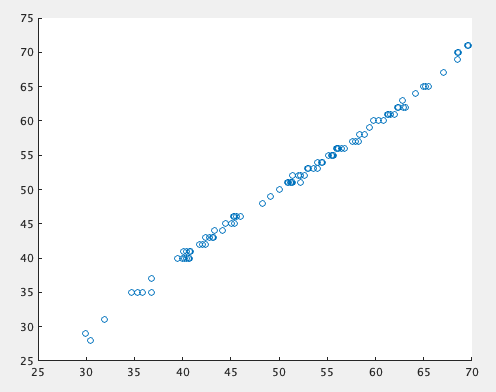
割と綺麗にいってる。なんもやってないのにこれ出てくるのは結構感動する。

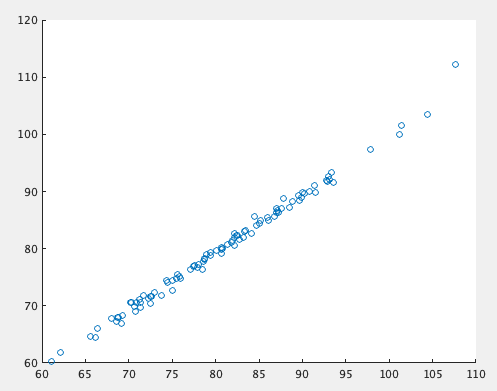
これを例えば目的変数を期間中のxの合計じゃなくて平均にしても（つまり Y{n, 1} = bias + sum(X{n,1})/T; に変えても）、全く同じネットワーク構造で散布図が

横軸が予測値yhat、縦軸が実測値Y

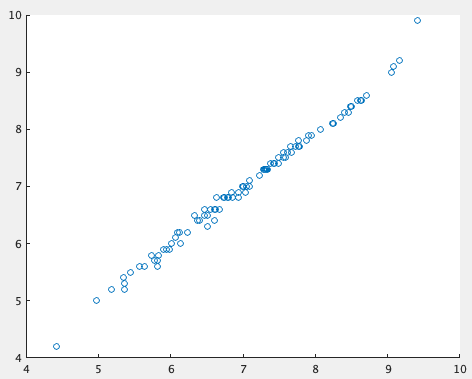
やっぱこういうのみると機械学習すげえなってなりますね。思考停止してもできそう。

重回帰に拡張する

1変数の線形結合取ってまあまあいい結果になるだけじゃつまんないですわね。重回帰にするだけならさっきのコードの最初のnvar=1を2以上にすればいいだけなんだけど、やはり隠れ層のユニット数は調整が必要で、

  • n_hidunit = 1
  • n_hidunit = 5

当然その数によって結果が変わってくる。3変数だろうと線形だから別に1ユニットで十分に予測できるにはできるんだけど、1ユニットでちゃんと綺麗な結果を出そうとするとEpoch増やさないとうまくいかない（今回のLSTMレイヤーにはtanhの活性化関数が設定されてるので当たり前なんだけど）。すると面倒くさがってユニット数を増やすことになる。

非線形重回帰に拡張する

たとえば対数とって

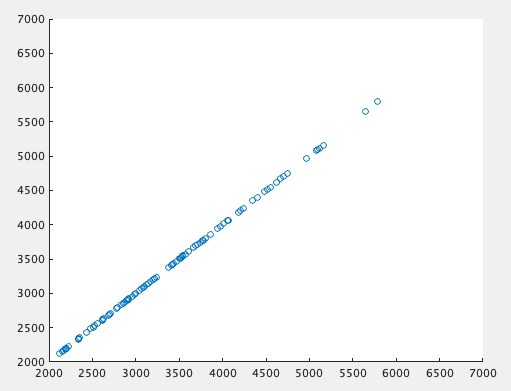
Y{n, 1} = log(bias + sum(coef*X{n, 1}));

とかにすると、これは結構簡単に予測できる。

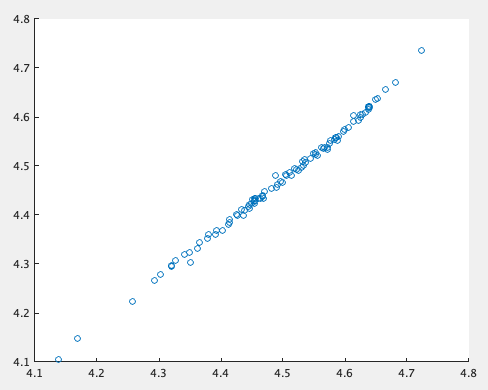
Epoch 6000でここまで綺麗に出る。

ただこれが

Y{n, 1} = (bias + sum(coef*X{n, 1}))^2;

になると、Epoch 5万とかでもまだ収束しない。T =10だぞ。7〜8万Epochぐらいまで回すとそれなりの結果になってくる。

  • ユニット数 10
  • ユニット数 20

まあ隠れ層とユニット数を増やせば理論的にはどんな非線形関数も近似できるわけだから、実際こうやって増やせばなんとかはなるわけだ。

ここまでのシミュレーションからわかることは、ユニット数とEpochを増やせばこれぐらいのデータの非線形近似は脳みそが空でもできるということですね。とはいえこんな単純なモデルにそんな10万弱のEpochかけるなんて計算資源と電力の無駄でしかないので、だから思考停止してデータを全部突っ込む類の分析が嫌いなんですね。人間がデータ見て構造を探索した上で時系列データをパネルデータまで集計して粒度落としたら回帰するまでもないことが見えてくると思うのだが。

余談

ちなみにParallel Computing ToolboxがあればGU計算とか並列計算とかやれるんだけど、それに関してはtrainingOptionsの中にExecutionEnvironmentを指定すれば良くて、’ExecutionEnvironment’,’parallel’なら並列計算、’ExecutionEnvironment’,’gpu’ならGPU計算が走るんだけど、まずRNNは並列計算には対応していない（エラー：再帰型ネットワークの並列学習はサポートされていません）。そしてGPU計算については、

畳み込みニューラル ネットワークの GPU サポートには、Compute Capability 3.0 以上の GPU デバイスが必要です。Parallel Computing Toolbox による GPU 高速化は、macOS version 10.14 (Mojave) 以降ではサポートされていません。以前の macOS バージョンに対するサポートは、将来の MATLAB リリースで削除される予定です。

だからできない（このmacの環境はCatalina 10.15.7）。

やっぱ解析環境そのものにmacOSなんか使うもんじゃないんだよな。こんな頻繁に仕様変更されるようなOSはダメなのよ。大人しくDockerかLinuxサーバーでも立ててそっちで計算させつつ、手元のデバイスはMacBook Airにでもしてモビリティを最優先にすべきなのだ。

あと今回はテストデータは当ててないけど、これは誤差項作らずに数値シミュレーションやってる関係でテストでも基本的にはほぼ同じ結果になるはずだし、正直ハイパラの調整した複数の予測結果を比較するとかならまだしも、単一のシミュレーションに対して絶対的な指標にもならないRMSEで汎化誤差出してもあんまり意味がないのでやっていません。そして機械学習をそれなりにやっていればこれぐらいのシミュレーションにノイズ乗せた時にテストデータでどれぐらい精度が落ちるかのイメージはつくようになってるはずというのもある。

使い方がわかったのであとは実データにあてて論文書くよ。